資料の活用 中央値 317860-資料の活用 中央値 求め方

中央値 最頻値 中1数学 資料の活用4 Youtube

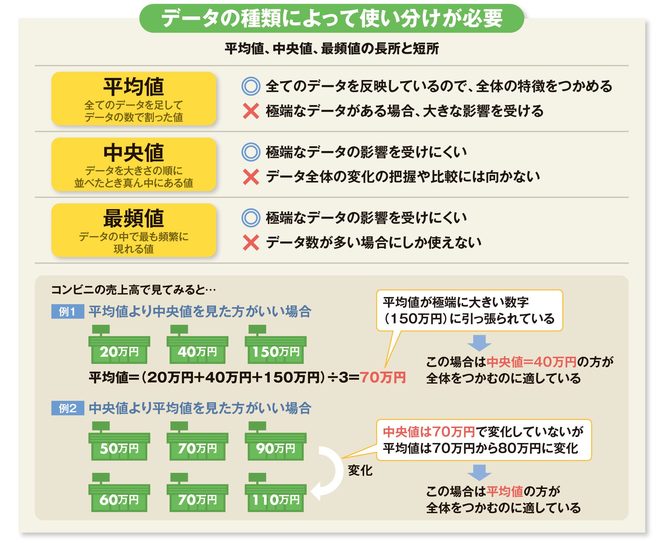
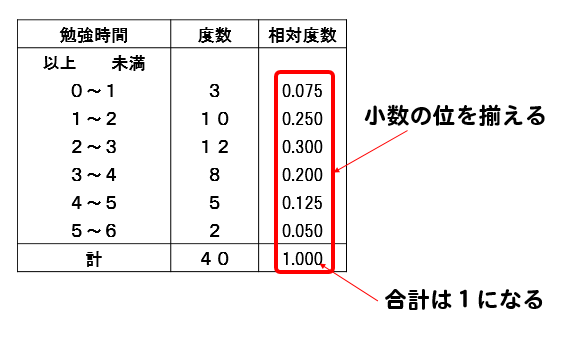
代表値 解説 各資料の値全体を代表している，つまり，資料全体の特徴を表している数値のことを代表値といい，次の3つがあります。 平均値（平均）：資料全体の数値の合計を，資料の全個数で割って得られる値で，次の式により求めることができます。最大の値は32分、 最小の値は3分なので 範囲 = 32 − 3 = 29 となる。 代表値 資料の特徴を表すために代表させる1つの値を 代表値 という。 代表値には 平均値、中央値、最頻値 などがある。 平均値 個々の資料の値の合計を資料の総数で割る。

資料の活用 中央値 求め方

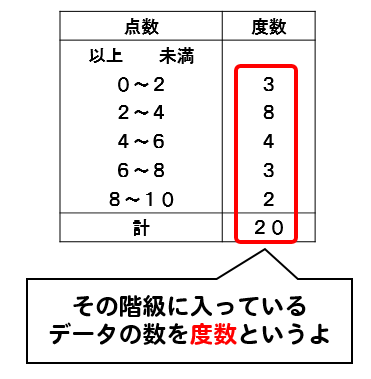
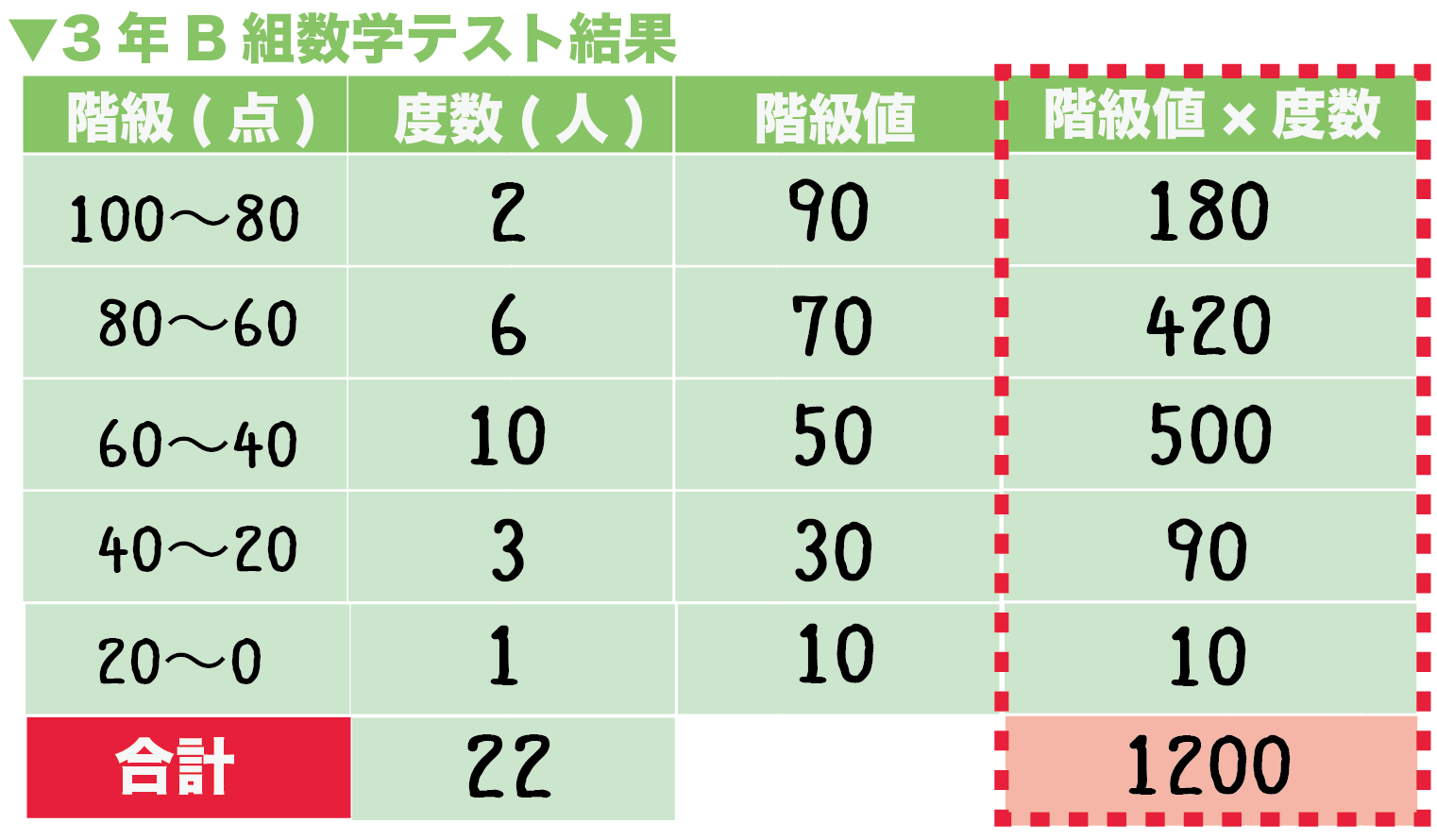
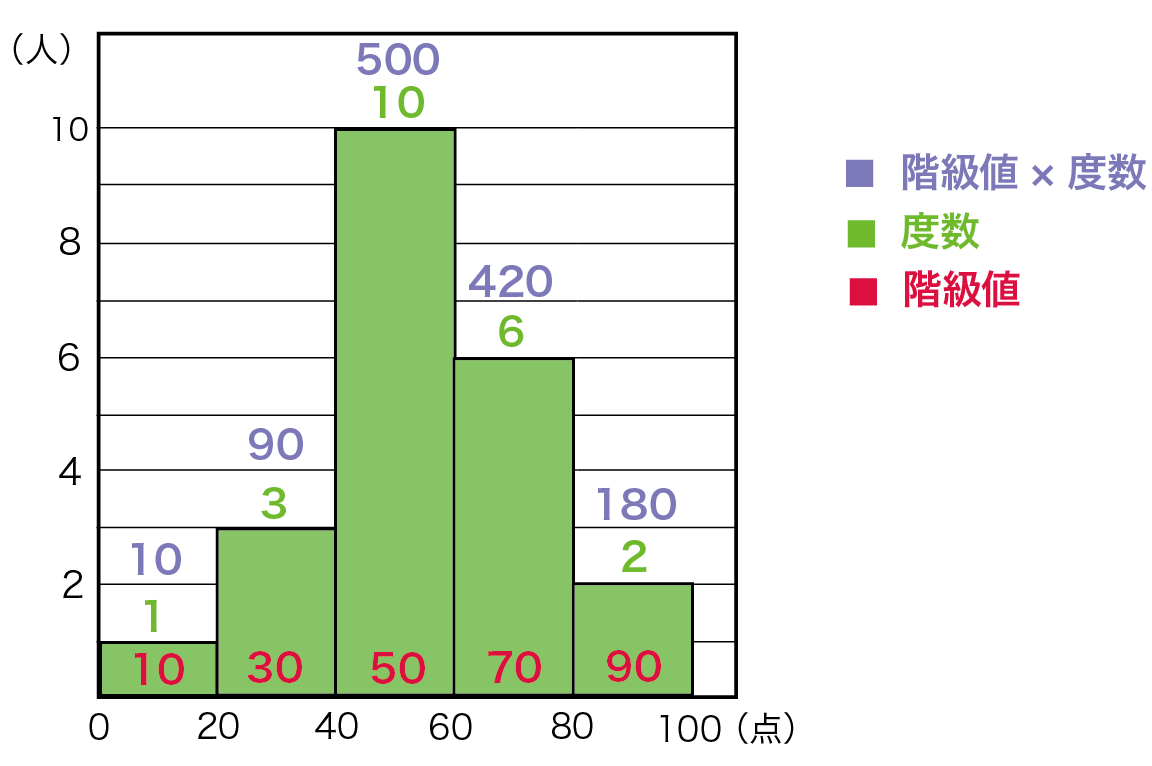
資料の活用 中央値 求め方- 階級値 ×度数の値を合計して、その値を度数の合計で割れば、平均値が出ます。 18/4/10 1−3の問題と解答の数値が一致していなかったので、プリントを入れかえました。 代表値 中央値 ：資料の数値を小さい順に並べたときに中央に位置する値 メジアンとD 資料の活用 (1) 目的に応じて資料を収集し，コンピュータを用いたりするなどして表やグラフに整理 し，代表値や資料の散らばりに着目してその資料の傾向を読み取ることができるように する。 ア ヒストグラムや代表値の必要性と意味を理解すること。

代表値 平均値 中央値 最頻値 の意味と違い 数学fun

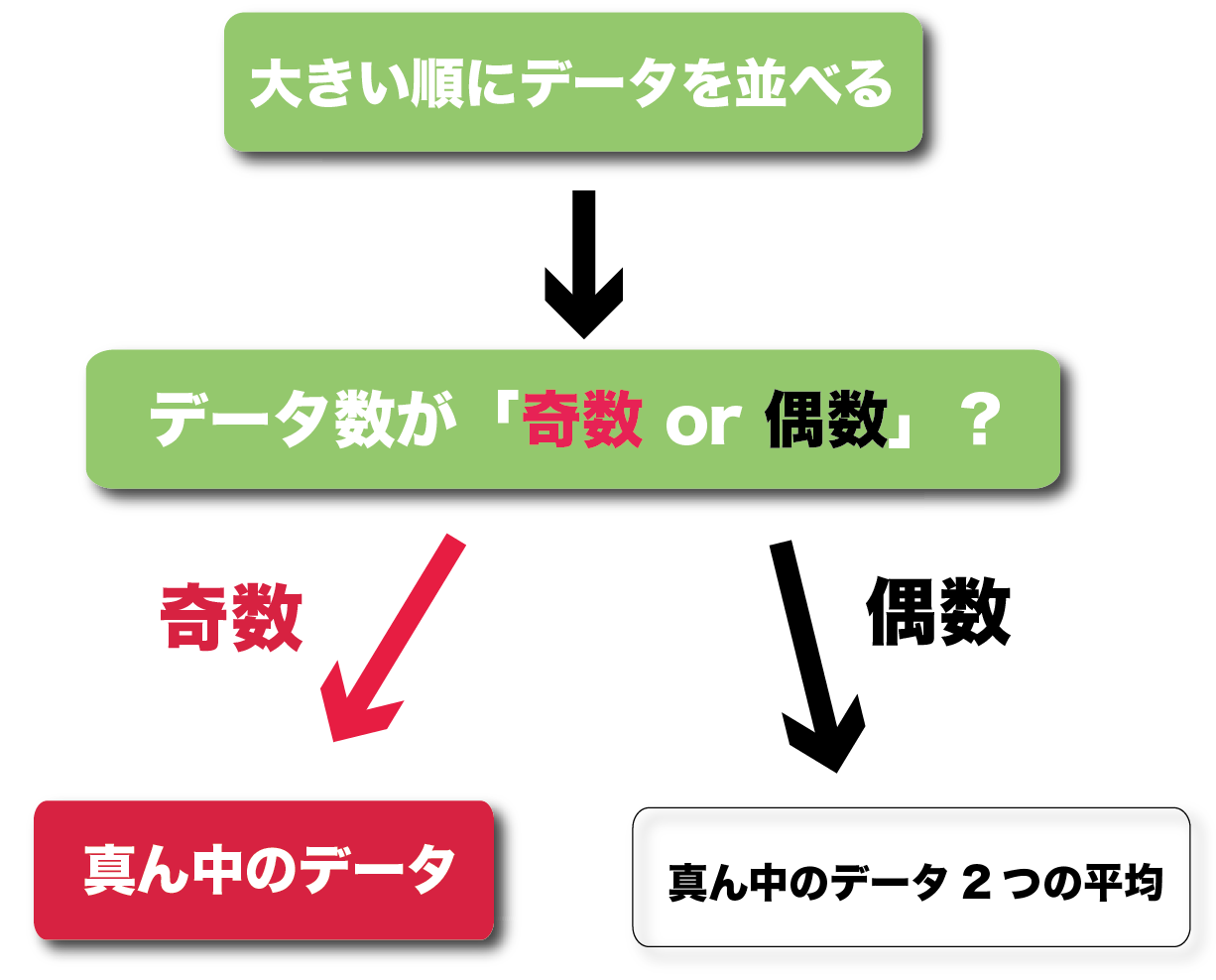
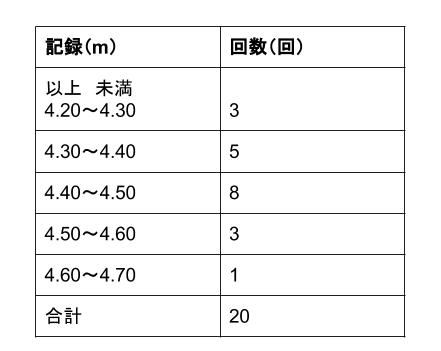
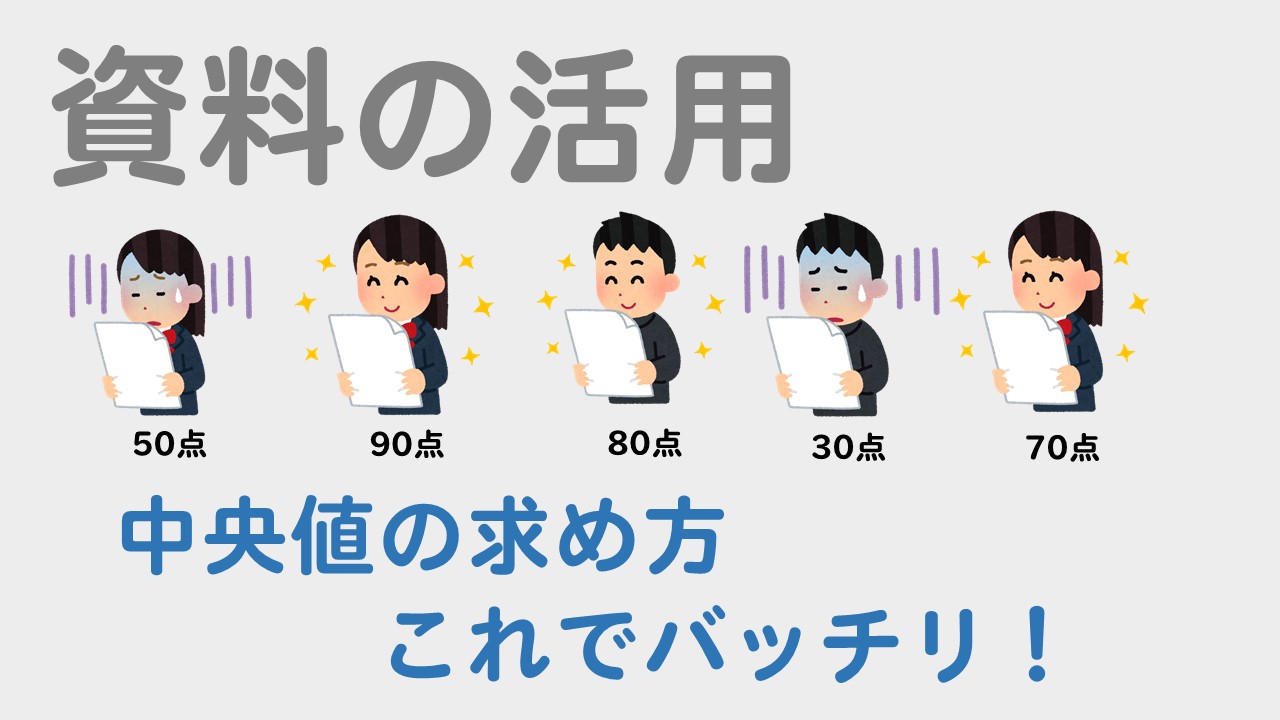
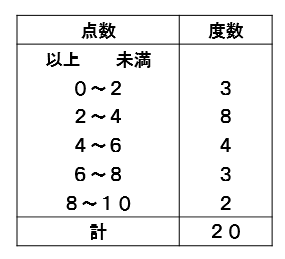
中央値 下の数値は、ある中学校の生徒名の通学時間である。 4，5，5，6，8，12，13，13，15，19 6，6，9，11，14，16，19，，21，27 （分） 中央値 資料の値を大きさの順に並べたときに、⑩⑪統計資料 の活用Ⅱ 活用問題③ ⑩⑪統計的手法を活用して，問題を解決する。 ㋐ ㋐ ㋑ ㋒ 12 ⑫章の問題 ⑫教科書p250に取り組む。 3 本時案 （1）本時の目標 代表値の意味を理解し，資料から値を求めることができる。平均値= 値の合計 資料の総数 度数分布表から平均を求める場合、各階級の資料の値はすべて階級値として計算する。 計算(1475×××××2)÷=1565 中央値を求めよ。 中央値とは資料を大きさの順に並べたときのちょうど真ん中の値

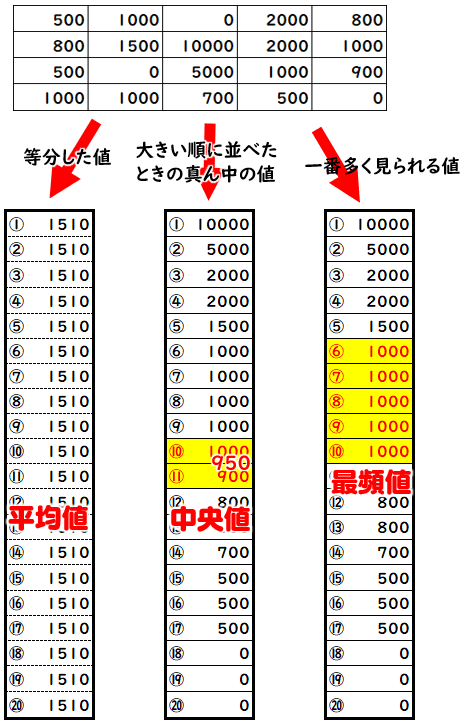
 では、理解を深めるために最頻値を求める問題に挑戦してみましょう。 次の資料の最頻値を求めなさい。 それぞれの値が何個ずつあるのか数えてみましょう。 10は1個、は3個、30は1個、40は2個、50は1個 すると、が一番多いってことが分かりますね1〜2年 資料の活用 2 3 ある数a の小数第2位を四捨五入したら37になっ た。このとき，a の値の範囲を不等号を使って表せ。 〔＇14 鹿児島〕 4 次の表は，魚釣りをしていた50人に対して，釣れ 単元 資料の分析,資料の活用,近似値と有効数字, 「中1の7章をまとめました！ 度数分布表や代表値などが書かれています。 いいね、フォローよろしくお願いします🙇‍♂️」, 学年 中学1年生, キーワード 中1,数学,度数分布表,ヒストグラム,柱状グラフ,相対度数,ラマ,代表値,平均値,中央値

資料の活用 中央値 求め方のギャラリー

各画像をクリックすると、ダウンロードまたは拡大表示できます

授業実践記録 数学 資料の活用 啓林館	授業実践記録 数学 資料の活用 啓林館	授業実践記録 数学 資料の活用 啓林館
授業実践記録 数学 資料の活用 啓林館	授業実践記録 数学 資料の活用 啓林館	授業実践記録 数学 資料の活用 啓林館
授業実践記録 数学 資料の活用 啓林館	授業実践記録 数学 資料の活用 啓林館	授業実践記録 数学 資料の活用 啓林館
授業実践記録 数学 資料の活用 啓林館	授業実践記録 数学 資料の活用 啓林館	授業実践記録 数学 資料の活用 啓林館
授業実践記録 数学 資料の活用 啓林館	授業実践記録 数学 資料の活用 啓林館	授業実践記録 数学 資料の活用 啓林館
授業実践記録 数学 資料の活用 啓林館	授業実践記録 数学 資料の活用 啓林館	授業実践記録 数学 資料の活用 啓林館
授業実践記録 数学 資料の活用 啓林館	授業実践記録 数学 資料の活用 啓林館	授業実践記録 数学 資料の活用 啓林館
授業実践記録 数学 資料の活用 啓林館	授業実践記録 数学 資料の活用 啓林館	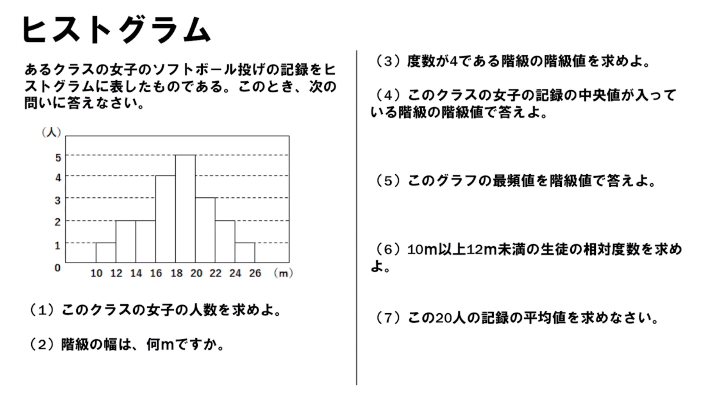授業実践記録 数学 資料の活用 啓林館
授業実践記録 数学 資料の活用 啓林館	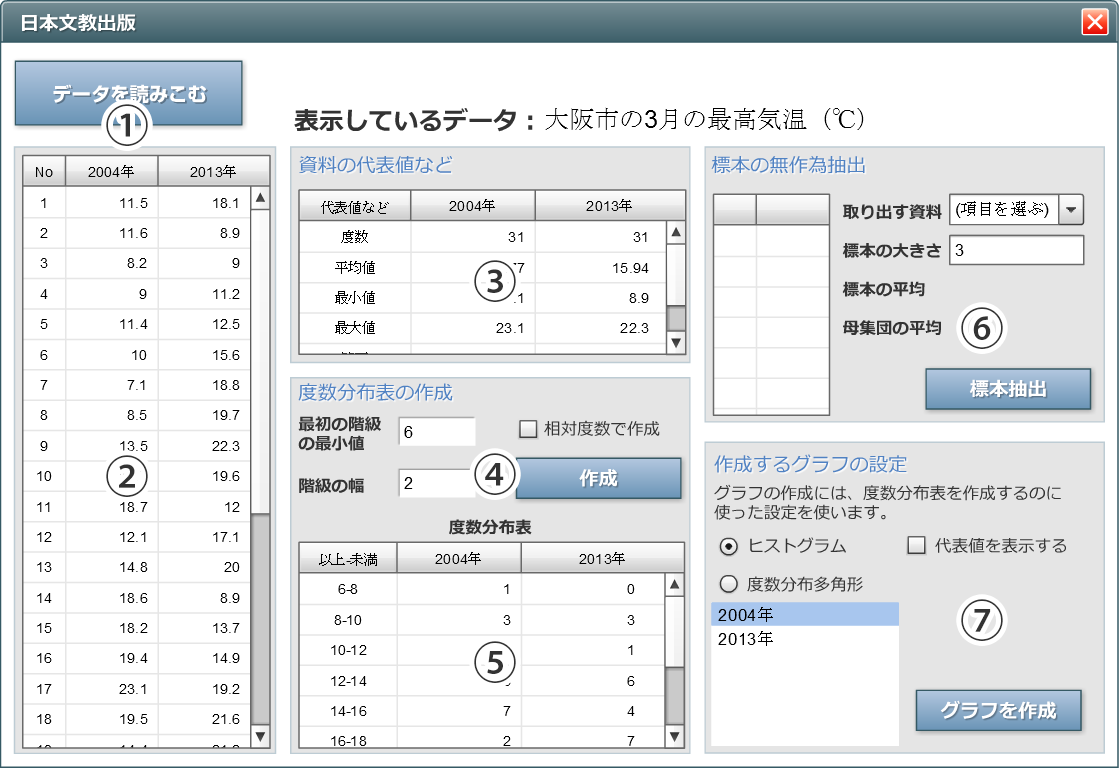授業実践記録 数学 資料の活用 啓林館	授業実践記録 数学 資料の活用 啓林館
授業実践記録 数学 資料の活用 啓林館	授業実践記録 数学 資料の活用 啓林館	授業実践記録 数学 資料の活用 啓林館
授業実践記録 数学 資料の活用 啓林館	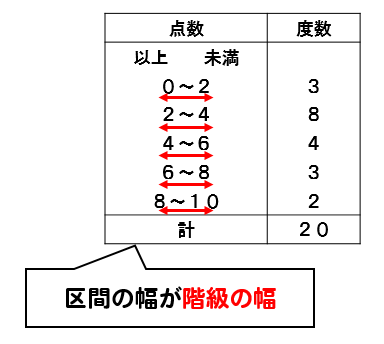授業実践記録 数学 資料の活用 啓林館	授業実践記録 数学 資料の活用 啓林館
授業実践記録 数学 資料の活用 啓林館	授業実践記録 数学 資料の活用 啓林館	授業実践記録 数学 資料の活用 啓林館
授業実践記録 数学 資料の活用 啓林館	授業実践記録 数学 資料の活用 啓林館	授業実践記録 数学 資料の活用 啓林館
授業実践記録 数学 資料の活用 啓林館	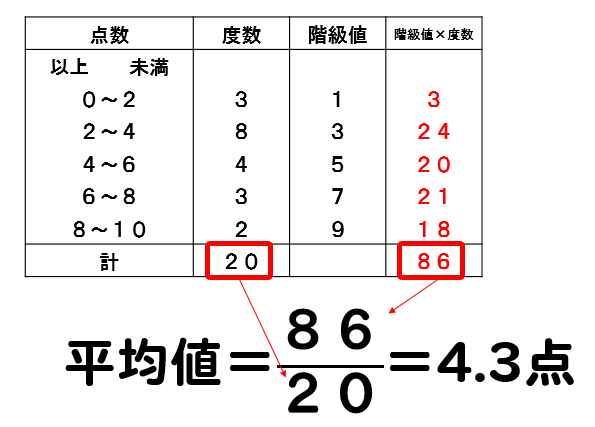授業実践記録 数学 資料の活用 啓林館	授業実践記録 数学 資料の活用 啓林館
授業実践記録 数学 資料の活用 啓林館	授業実践記録 数学 資料の活用 啓林館	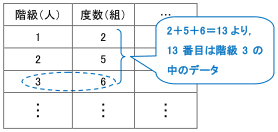授業実践記録 数学 資料の活用 啓林館
授業実践記録 数学 資料の活用 啓林館	授業実践記録 数学 資料の活用 啓林館	授業実践記録 数学 資料の活用 啓林館
授業実践記録 数学 資料の活用 啓林館	授業実践記録 数学 資料の活用 啓林館	授業実践記録 数学 資料の活用 啓林館
授業実践記録 数学 資料の活用 啓林館	授業実践記録 数学 資料の活用 啓林館	授業実践記録 数学 資料の活用 啓林館
授業実践記録 数学 資料の活用 啓林館	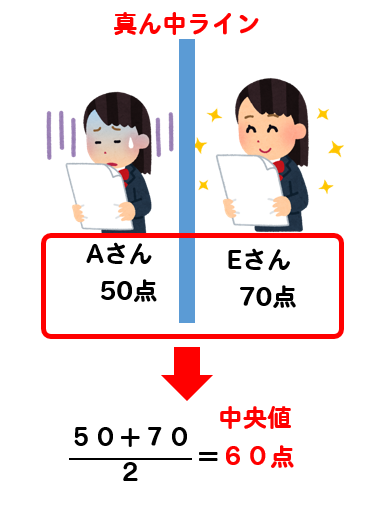授業実践記録 数学 資料の活用 啓林館	授業実践記録 数学 資料の活用 啓林館
授業実践記録 数学 資料の活用 啓林館	授業実践記録 数学 資料の活用 啓林館	授業実践記録 数学 資料の活用 啓林館
授業実践記録 数学 資料の活用 啓林館	授業実践記録 数学 資料の活用 啓林館	授業実践記録 数学 資料の活用 啓林館
授業実践記録 数学 資料の活用 啓林館	授業実践記録 数学 資料の活用 啓林館	授業実践記録 数学 資料の活用 啓林館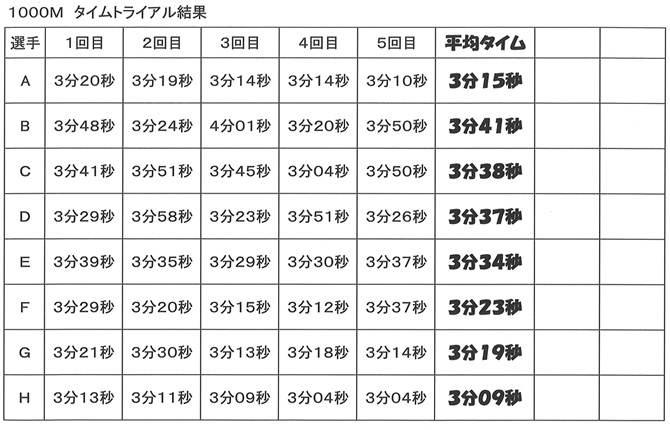
授業実践記録 数学 資料の活用 啓林館	授業実践記録 数学 資料の活用 啓林館	授業実践記録 数学 資料の活用 啓林館
授業実践記録 数学 資料の活用 啓林館	授業実践記録 数学 資料の活用 啓林館	授業実践記録 数学 資料の活用 啓林館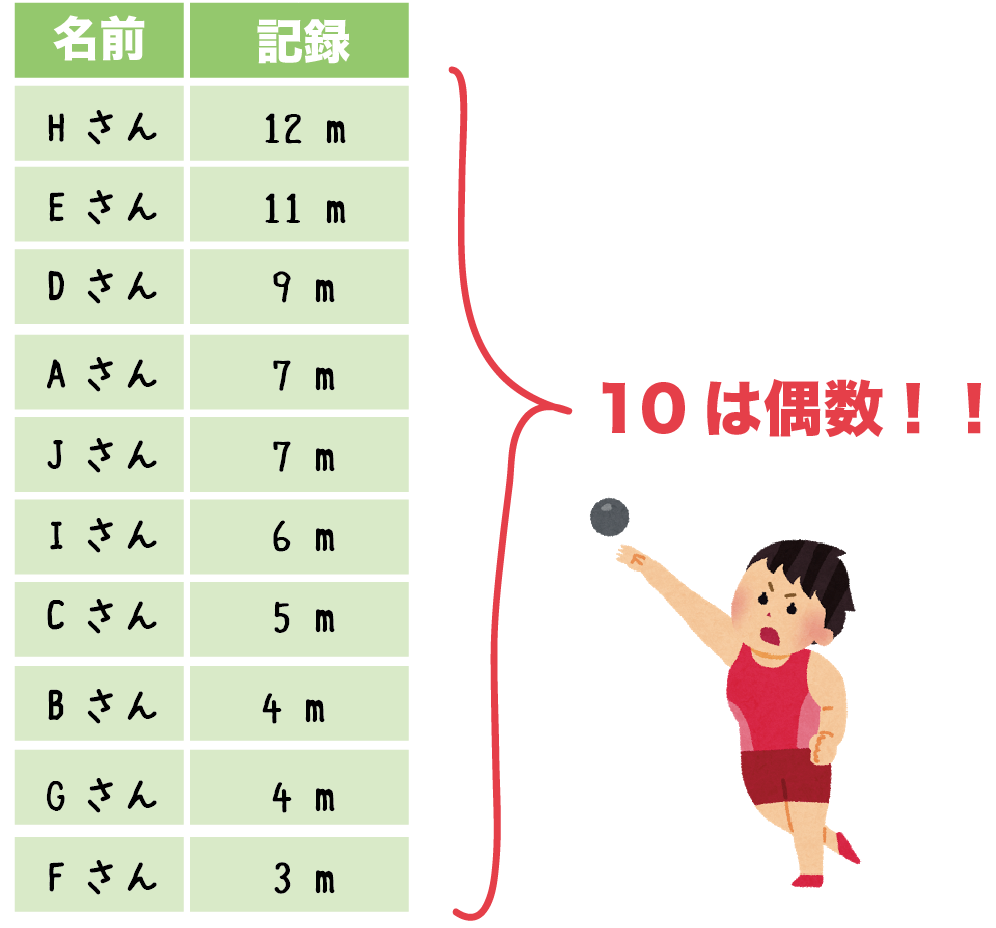
授業実践記録 数学 資料の活用 啓林館	授業実践記録 数学 資料の活用 啓林館	授業実践記録 数学 資料の活用 啓林館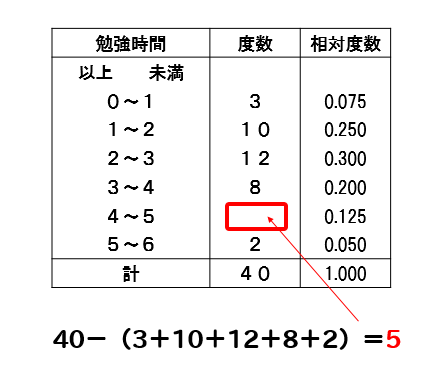
授業実践記録 数学 資料の活用 啓林館	授業実践記録 数学 資料の活用 啓林館	授業実践記録 数学 資料の活用 啓林館
授業実践記録 数学 資料の活用 啓林館	授業実践記録 数学 資料の活用 啓林館	授業実践記録 数学 資料の活用 啓林館
授業実践記録 数学 資料の活用 啓林館	授業実践記録 数学 資料の活用 啓林館	授業実践記録 数学 資料の活用 啓林館
授業実践記録 数学 資料の活用 啓林館	授業実践記録 数学 資料の活用 啓林館	授業実践記録 数学 資料の活用 啓林館
授業実践記録 数学 資料の活用 啓林館	授業実践記録 数学 資料の活用 啓林館	授業実践記録 数学 資料の活用 啓林館
授業実践記録 数学 資料の活用 啓林館	授業実践記録 数学 資料の活用 啓林館	授業実践記録 数学 資料の活用 啓林館
授業実践記録 数学 資料の活用 啓林館	授業実践記録 数学 資料の活用 啓林館	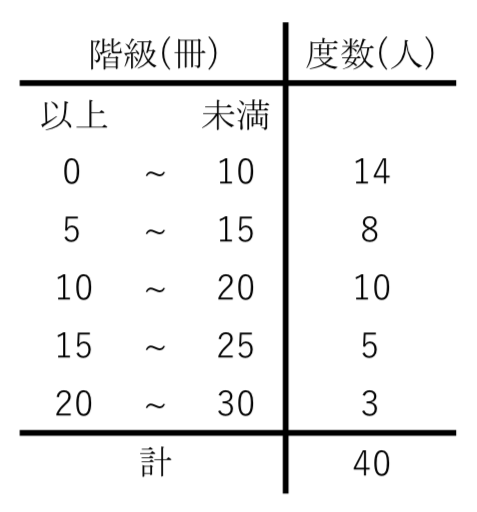授業実践記録 数学 資料の活用 啓林館
授業実践記録 数学 資料の活用 啓林館	授業実践記録 数学 資料の活用 啓林館	授業実践記録 数学 資料の活用 啓林館
授業実践記録 数学 資料の活用 啓林館	授業実践記録 数学 資料の活用 啓林館	授業実践記録 数学 資料の活用 啓林館
授業実践記録 数学 資料の活用 啓林館	授業実践記録 数学 資料の活用 啓林館

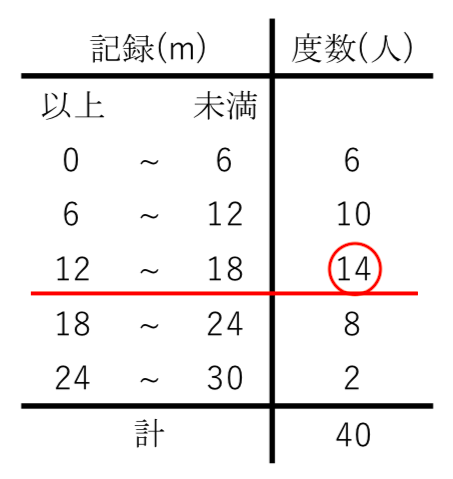
代表値 資料の値全体を1つの値で代表させ、これを基準にして、ものごとを考えたり判断したりする ことがある。このようなとき、資料の値全体を代表する値のこと。 中央値 （メジアン） 資料の値を大きさの順に並べたとき、その中央の値のこと。 最頻値資料の個数は18個で,偶数なので,中央値は中央にある 2つの値の平均値になります。 18の中央にある2つは9番目と10番目なので,中央値が 含まれる階級は,8m以上12m未満。 ※階級に幅があるので,中央値を求めることはできません。 16m以上m未満までの人数は,3人

Incoming Term: 資料の活用 中央値 求め方, 資料の活用 中央値,